Wissenswerte Informationen über den Edelopal
Opal - Natürlicher Edelopal, Opalsynthesen und Opal-Imitationen Das Farbspiel
Edelopal mit Farbspiel aus Australien (Makroaufnahme)

Makroaufnahme eines australischen Opals mit Farbspiel
Das Farbspiel des Opals
Eine StrukturfarbeSchon früh beschäftigten sich Wissenschaftler mit der Ursache des Farbspiels des Edelopals.
Doch gebührt nicht den Australiern die Ehre, als erste die Farbursache ihres Nationalsteins erforscht zu haben, sondern verschiedenen europäischen Wissenschaftlern.
Eine der ersten Veröffentlichungen erschien bereits 1845 von Sir Brewster [1]. In seinem Artikel "On the Cause of the Colours in Precious Opal" (Edinburgh New Philosophical Journal, 1845) schreibt er:
"...the colorific planes or patches consist of minute pores or vacuities arranged in parallel lines, and that such planes are placed close to each other, so as to occupy a space with three dimensions...
Nahezu 90 Jahre danach (1932) veröffentlichte der deutsche Wissenschaftler E. Baier in seinem Werk "Die Optik der Edelopale" Überlegungen auf der Basis optischer Untersuchungen, die sich schließlich als richtig erwiesen [2]. Baier schlussfolgerte als erster (ohne Kenntnis des inneren Aufbaus), dass das Farbspiel des Edelopals eine Beugungserscheinung an "irgendwelchen dreidimensionalen, lichtoptisch wirksamen, periodischen Systemen" sein muss. Zitat:
"Die Auswahl der Farbe aus dem Weiß des einfallenden Lichtes geht dabei ganz in der Art der Braggschen Reflexion an Gitterebenen vor sich. Den kurzwelligen Reflexen entspricht dann also eine dichtere Ebenenfolge als den langwelligen"
Sir Raman bestätigte die Annahme eines regelmäßigen inneren Aufbaus 1953 in seiner Veröffentlichung "The structure of opal and the origin of its iridescence":
"...The optical behaviour of opal thus compels us to recognise the existence of a remarkably perfect periodicity in its structure..."
"...it is clear that the phenomena observed have a common origin, namely, the existence of regular optical stratifications within the material..."
Wenngleich Raman von einer Wechsellagerung aus Hoch- und Tief-Cristobalit ausging, waren er, Baier und Brewster der wahren Ursache des Farbspiels von Edelopalen sehr nahe.
Gebeugtes Licht
Die Bragg'sche GleichungEs dauerte noch einmal 30 Jahre bis Luck, Klier und Wesslau anhand synthetischer kolloidkristalliner Systeme die heute grundlegende "korrigierte Braggsche Gleichung" entwickelten [3].
Im gleichen Jahr gelang der experimentelle Nachweis des dreidimensional periodischen Aufbaus natürlicher Edelopale mit Hilfe elektronenmikroskopischer Aufnahmen, die von Pense präsentiert worden sind [4].
Das Prinzip der Beugung als Ursache des Farbspiels kann mit diesen Erkenntnissen an einer Stapelfolge dichtestgepackter Ebenen (fcc, A-B-C) wie folgt beschrieben werden.
Die allgemeine Form der Bragg’schen Gleichung lautet:
m • λ= 2 • d • sin θ
m - Beugungsordnung
λ - Wellenlänge
d - Netzebenabstand
θ - Glanzwinkel
Im Gegensatz zur Röntgenbeugung mit einem Brechungsindex von n~1 muss die Bragg’sche Gleichung aufgrund der Wechselwirkung mit Licht entsprechend korrigiert werden [3].
Die Wellenlänge λ (innerhalb der Probe) ist zu ersetzen durch λ= λ0 / n, mit n als effektivem Brechungsindex der Probe und λ0 (Wellenlänge außerhalb der Probe):
m • λ0 = 2 • d • n sin θ
Zur Beschreibung des Verhaltens des Lichtes an einer Phasengrenze von Materialien mit unterschiedlichem Brechungsindex (n1, n2) unter einem Einfallswinkel α und dem Brechungswinkel β dient das Gesetz von Snellius:
n1 • sin α = n2 • sin β
Werden beide Gesetze kombiniert, so lässt sich mit der resultierenden Gleichung aus spektroskopischen Messungen der entsprechende Netzebenenabstand und damit die Gitterkonstante (bzw. die Größe der Partikel) ermitteln. Die korrigierte Version der Bragg’schen Gleichung lautet nun:
m • λ0 = 2 • d √(n22-n21 • cos2 θ)
An Luft mit n=1 vereinfacht sich die Gleichung deutlich:
m • λ0 = 2 • d √(n22 • cos2 θ)
Der Brechungsindex n2 ist hier der effektive Brechungsindex neff des Materials, der sich bei einer Dichtestpackung sphärischer Partikel (74% Raumerfüllung) wie folgt ergibt:
neff = √(0,74 n2Kugel+ 0,26n2Matrix)
Die Matrix ist hier das Material im Raum zwischen den Partikeln.
Für den Netzebenenabstand d gilt für eine Dichtestpackung aus Partikeln eines Durchmessers D:
d = √2/3 • D
Es resultiert damit folgende Gleichung:
m • λ0 = 1,633 • D √n2eff - cos2 θ
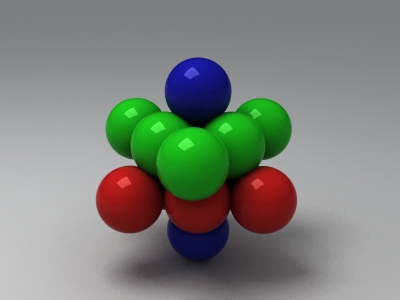
Kubische Dichtestpackung, ABC-Stapelfolge
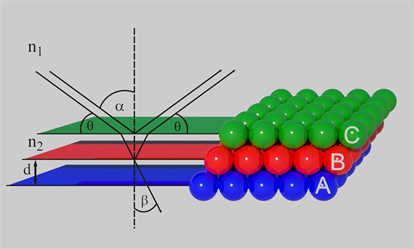
Bragg-Beugung an einer kubischen Dichtestpackung
ABC-Stapelfolge, Raumgruppe Fm3m
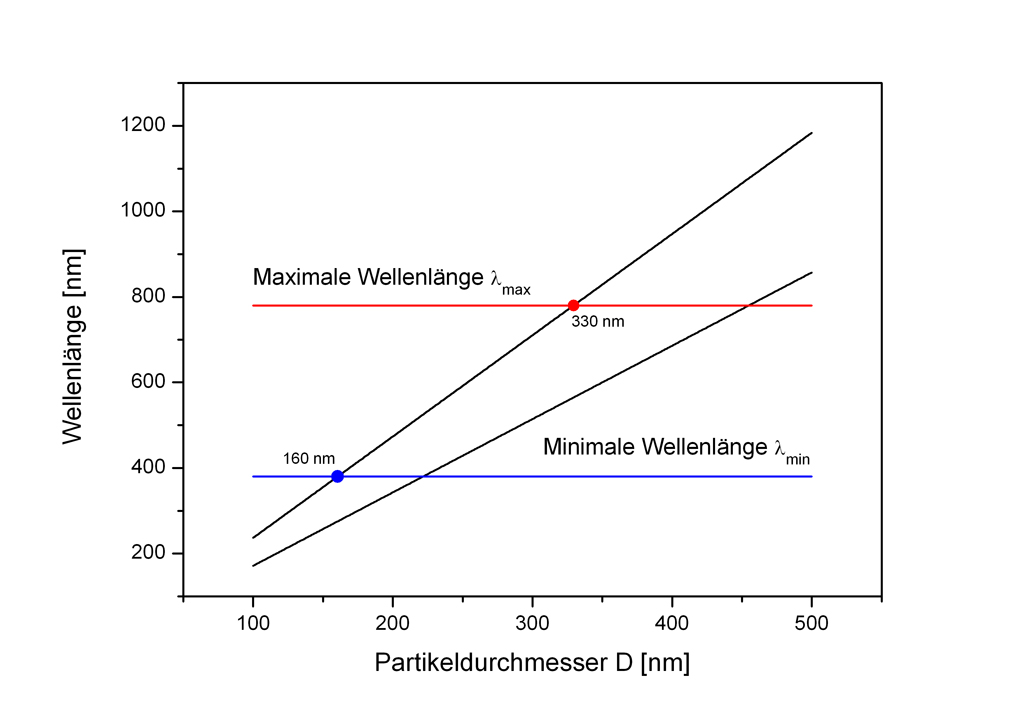
Abhängigkeit des gebeugten Wellenlängenbereichs vom Partikeldurchmesser D
Opal - Farbspiel
FaktorenDas Farbspiel des Edelopals ist somit strukturell bedingt und abhängig von folgenden Faktoren:
1. Größe der Partikel
2. Brechungsindex der Partikel
3. Brechungsindex der Matrix
4. Füllungsgrad des Porenraums
Unter der Annahme, dass der intensivste Reflex betrachtet wird (m=1) und mit einem effektivem Brechungsindex des Opals von n=1,45 läßt sich aus der letzten Gleichung ermitteln, ab welcher Partikelgröße überhaupt ein Farbspiel auftritt und bei welchem Durchmesser das Farbspiel hinsichtlich der gebeugten Wellenlängen am umfangreichsten ist [5].
In der Grafik ist zunächst der Bereich des sichtbaren Lichts markiert (380 - 780nm, rote und blaue horizontale Linien). Die schwarzen Linien markieren die minimale, bzw. maximale Wellenlänge bei entsprechendem Kugeldurchmesser.
Eingetragen ist des Weiteren der minimale Partikeldurchmesser, bei dem noch ein Farbspiel erkennbar ist (160nm, Wellenlänge 380nm - Violett), sowie der Partikeldurchmesser, bei dem das Spektrum der gebeugten Wellenlängen am umfangreichsten ist (330nm, Wellenlängenbereich von ca. 565nm - 780nm).
Literatur.
[1] Brewster, D. (1845): "On the Cause of the Colours in Precious Opal", Edinburgh New Philosophical Journal, 38, 385-386.
[2] Baier, E. (1932): "Die Optik der Edelopale", Zeitschrift für Kristallographie, A(81), 183-218.
[3] Luck, W., M. Klier, et al. (1963): "Kristallisation übermolekularer Bausteine." Naturwissenschaften, 50(14), 485-494.
[4] Pense, J. (1963): "Elektronenmikroskopischer Beitrag zur Optik der Edelopale", Jahrestagung der Deutschen und Österreichischen Mineralogischen Gesellschaft, 41, 166.
[5] Wollaert, E., Vochten, R., van Landuyt, J. (1990): "Characterisation of gem opal and inferior opal qualities by means of electron microscopy", Zeitschrift der Deutschen Gemmologischen Gesellschaft, 39, 4, 211-223.